딥러닝이 나오기 이전에 많이 사용되고 좋은 성능을 보여준 서포트 벡터 머신에 대해 리뷰하겠다. 글의 내용은 책 핸즈온 머신러닝을 참고하여 작성했다.
0. SVM이란
SVM(Support Vector Machine)이란, 매우 강력한 머신러닝 알고리즘으로 머신러닝을 배운 사람이라면 반드시 알고 있어야 하는 모델이다. 선형이나 비선형 분류, 회귀, 이상치 탐지에도 사용할 수 있는 다목적 머신러닝 알고리즘으로 특히 분류에서 성능이 뛰어나기 때문에 주로 분류에서 많이 사용된다.

위 그림에서 Separating Hyperplane은 일종의 Decision Boundary 결정 경계이다.
Decision Boundary란 분류를 하기 위한 기준 선이라고 생각하면 된다. 지금은 간단한 2-dimension에서의 Decision Boundary라 선 형태로 나타나지만, 차원이 계속 늘어나게 된다면 평면이 되며 이를 Hyperplane 초평면이라고 부른다.
다음으로 점선 위에 있는 결정경계와 가장 가까이 있는 데이터들을 Support Vector라고 한다. 이 Support Vector만을 가지고 SVM이 분류 및 회귀를 수행하기 때문에 아무리 많은 train data가 있더라도 게산량은 줄어든다.
Margin은 이러한 Support Vector와 결정 경계와의 간격을 말한다. 가장 최고로 잘 분류할 수 있는 Decision Boundary를 찾기 위해서 Margin이 가장 Maximium이 되게 해야 한다. 이 때 Support Vector는 최소 2개 이상이어야 한다.
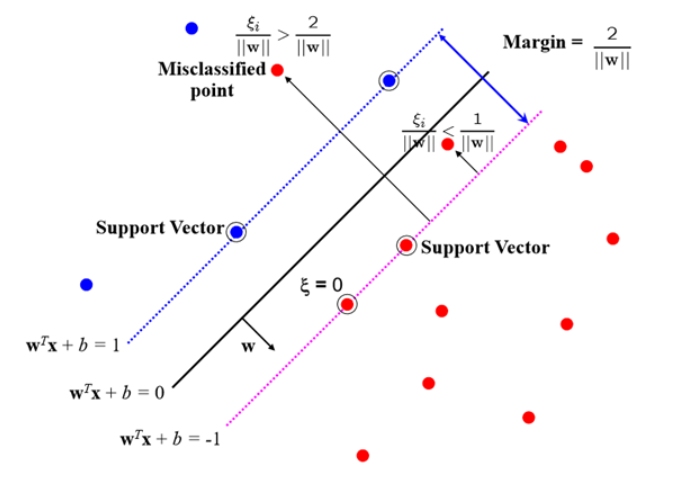
SVM은 $Wx + b = 0$이라는 Decision Boundary를 찾은 후 새로운 데이터가 $x$에 input으로 들어간 후 양/음에 따라 class를 분류하게 된다. 이 때 margin은 Decision Boundary에서 법선 벡터를 통해 구할 수 있으며, 간단한 계산과정을 거치면 $Margin(width) = \frac{2}{||w||}$이라는 식에 도달하게 된다.
결국 margin을 최대화 하려면 벡터 $w$를 최소화 해야함을 알 수 있다. 여기서 $||w||$를 최소화 하는 것은 $||w||^2$을 최소화 하는 것과 같기 때문에 SVM도 결국 대부분의 머신러닝 알고리즘에서 최적화 방법으로 사용하고 있는 quadratic optimization을 거치게 된다.
다음으로 위 그림에서 **Slack Variable ξ**를 살펴보자.
$$ ξ_{n} = |t_{n} - y(x_{n})| $$
Slack Variable(ξ)이란, 직선을 그었을 때 내가 속한 클래스와 실제 y 값의 차이를 뜻한다. 슬랙 변수(Slack Variable)는 선형적으로 분류할 수 없는 경우에 오차를 허용해야 하는데 이 때 constraints를 완화해 overfitting 현상을 줄이기 위해 고안된 개념이다.
쉽게 말하면 Decision Boundary 양 옆의 경계선을 침범하여 틀린(오차인) 데이터이다. $ξ = 0$이면 정상적으로 분류된 경우, $0 < ξ < 1$ 또는 $ξ = 1$이면 마진이 작은 경우이고 $ξ > 1$이면 분류가 잘못된 경우이다.
1. 선형 SVM 분류
1.1 소프트 마진 분류

SVM은 마진의 크기를 최대화 하는 결정 경계를 찾아야 하는데 결국 이상치를 얼마나 허용할 건지에 따라 소프트 마진과 하드 마진으로 분류할 수 있다. 위 그림을 보면 이상치들이 마진 안에 어느정도 포함되도록 허용하고 있다. 이를 소프트 마진(Soft Margin)이라 한다. 좀 더 유연한 모델이라고 할 수 있다.
1.2 하드 마진 분류
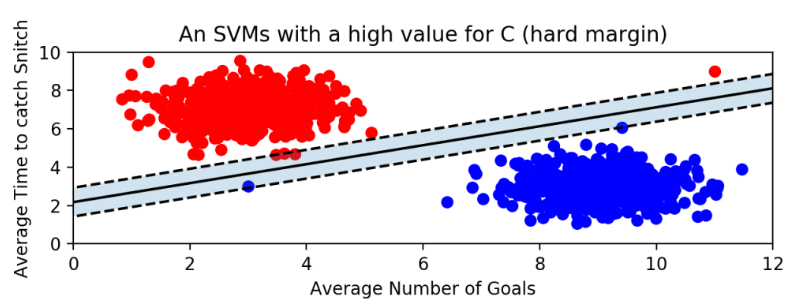
위 그림은 이상치에도 매우 민감하게 반응하여 하드 마진(Hard Margin)이라고 한다. 이렇게 개별적인 train data들을 다 놓치지 않고 기준을 까다롭게 적용한다. 이렇게 하드 마진의 경우 데이터가 선형적으로 구분될 수 있어야 제대로 작동하며, 이상치에 매우 민감하게 반응해 결정 경계와 마진을 형성하므로 일반화가 잘 되지 않아 overfitting 문제가 발생할 수 있다.
여기서 Regularization Parameter $C$를 통해 마진을 조절할 수 있다.
$$ L(w, ξ) = \frac{1}{2}||w||^2 + C\sum_{i=1}^{n}{ξ_{i}} $$
SVM이 최적화 시 이전에 살펴본 슬랙 변수까지 고려해 위와 같은 식으로 표현이 가능한데 위 식에서의 $C$는 일반화 목적으로 들어가는 일종의 penalty로 생각할 수 있다. 쉽게 말해 슬랙 변수를 얼마나 허용할 지에 대한 척도이다.
$C$가 큰 경우는 분류 기준을 까다롭게 한다는 뜻으로 정확히 분류하려고 할 것이다. 따라서 허용 오차의 개수가 작고 $||w||$에 집중하여 margin이 좁다. 반대로 $C$가 작은 경우 분류 기준이 관대하고 margin이 커진다.

위 그림을 보면 이해가 빠르다. $C$가 작을 경우 margin이 더 크고 오류를 더 많이 허용한다. 반대로 $C$가 큰 경우 margin이 굉장히 좁고 오류를 적게 허용한다. 이처럼 $C$를 통해 margin의 폭을 유연하게 조절할 수 있다.
2. 비선형 SVM 분류
2.1 다항식 커널
pass
2.2 유사도 특징

비선형 특성을 다루는 또 다른 방법은 각 샘플이 특정 랜드마크와 얼마나 닮았는 지 측정하는 유사도 함수로 계산한 특성을 추가하는 것이다. 예를 들어 1차원 데이터셋에 다음 값을 중앙값으로 가지는 두 개의 랜드마크 $x_{2} = -2$와 $x_{3} = 1$을 추가하자. 그리고 $𝛄 = 0.3$인 가우시안 방사 기저 함수(RBF)를 유사도 함수로 정의하면 다음과 같다.
$$0 \leq ϕ_{γ}(x,𝓁) = exp(-γ||x-𝓁||^2) \leq 1$$
예시로 $x_{1} = -1$ 샘플을 봐보자. $x_{1}$은 첫 번째 랜드마크인 $x_{2}$에 대해 1만큼 떨어져 있고, 두 번째 랜드마크인 $x_{3}$에 대해 2만큼 떨어져 있다. 그래서 $x_{2} = exp(-0.3 \times 1^2) \approx 0.74$와 $x_{3} = exp(-0.3 \times 2^2) \approx 0.30$이고, 이렇게 계산된 값들을 위 그림의 오른쪽 그래프에 그려 선형적으로 구분이 가능해졌다.
2.3 가우시안 RBF 커널
다항 특성 방식과 마찬가지로 유사도 특성 방식도 머신러닝 알고리즘에 유용하게 사용될 수 있다. 추가 특성을 모두 계산하려면 연산 비용이 많이 드는데 특히 훈련 세트가 클 경우 더 그렇다. 여기에서 커널 트릭이 한 번 더 SVM의 마법을 만든다. 유사도 특성을 많이 추가하는 것과 같은 비슷한 결과를 얻을 수 있다. 가우시안 RBF 커널을 사용한 SVC 모델은 다음과 같다.
rbf_kernel_svm_clf = Pipeline([
('scaler', StandardScaler()),
('svm_clf', SVC(kernel='rbf', gamma=5, C=0.001))
])
rbf_kernel_svm_clf.fit(X, y)이 코드에 나타난 모델의 학습 결과는 다음 그림의 왼쪽 아래 그래프이며 여러가지 γ와 C를 바꾸어 훈련시켰다.

γ를 증가시키면 종 모양 그래프가 좁아져서 각 샘플의 영향 범위가 작아진다. 결정 경계가 조금 더 불규칙해지고 각 샘플을 따라 구불구불하게 휘어진다. 반대로 작은 γ은 넓은 종 모양 그래프를 만들어 샘플이 넓은 범위에 걸쳐 영향을 주므로 결정 경계가 더 부드러워진다. 결국 γ가 규제의 역할을 하는데 모델이 과대적합일 경우엔 감소시켜야 하고 과소적합일 경우엔 증가시켜야 한다. (C와 비슷하다.)
2.4 시간 복잡도

3. SVM 회귀
SVM 알고리즘은 범용성이 좋은데 앞서 이야기한 선형, 비선형 분류뿐만 아니라 선형, 비선형 회귀에도 사용할 수 있다. SVM을 분류가 아니라 회귀에 적용하는 방법은 목표를 반대로 하는 것이다. SVM 분류는 일정한 마진 오류 안에서 두 클래스 간의 도로 폭이 가능한 최대가 되도록 하는 대신, SVM 회귀는 제한된 마진 오류(즉, 도로 밖의 샘플) 안에서 도로 안에 가능한 많은 샘플이 들어가도록 학습한다. 도로의 폭은 ɛ으로 조절하는데 값이 커지면 마진이 넓어지고 값이 작아지면 마진이 좁아진다.

위 그림은 무작위로 생성한 선형 데이터셋에 훈련시킨 두 개의 선형 SVM 모델을 보여주는데 왼쪽은 마진을 크게, 오른쪽은 마진을 작게 만들었다. 왼쪽 그래프 코드는 다음과 같다.
from sklearn.svm import LinearSVR
svm_reg = LinearSVR(epsilon=1.5)
svm_reg.fit(X, y)
비선형 회귀 작업을 처리하려면 커널 SVM 모델을 사용하는데 위 그림은 임의의 2차 방정식 형태의 훈련 세트에 2차 다항 커널을 사용한 SVM 회귀를 보여준다. 왼쪽 그래프는 규제가 거의 없고(즉, 아주 큰 C), 오른쪽 그래프는 규제가 훨씬 많다(즉, 작은 C). 다음 코드는 왼쪽 그래프를 그리는 모델이다.
from sklearn.svm import SVR
svm_poly_reg = SVR(kernel='poly', degree=2, C=100, epsilon=0.1)
svm_poly_reg.fit(X, y)'~2023' 카테고리의 다른 글
| [CS231n] Lecture 4. Backpropagation and Neural Networks (0) | 2023.04.25 |
|---|---|
| [CS231n] Lecture 8. Deep Learning Software (0) | 2023.04.25 |
| [CV] Object Detection 검증 지표 (0) | 2023.04.25 |
| [후기] 데이터청년캠퍼스 2022 (3/3) - 가자 원주혁신도시로 ! (0) | 2023.04.25 |
| [후기] 데이터 청년 캠퍼스 2022 (2/3) - 경남대.. 그리고 힘들었던 프로젝트 결정 (0) | 2023.04.25 |


