Table of contents
1. Introduction
1.1 Forward propagation
1.2 Backward propagation
1.3 computational graph
1.4 chain rule
1.5 Partial Derivative
2. Backward propagation
2.1 Backward propagation
2.2 Gradients for Vector
3. Neural Networks
3.1 Neural Networks
1. Introduction

미분을 통해 최적화를 하는 방법에는 크게 두가지가 있었습니다.
- Numerical gradient (수치적 미분) : 속도가 느리고 근사치를 찾는 방법임.
- Analytic gradient (해석적 미분) : 빠르고 정확하지만 실수하기 쉬움.
이번 lecture 4에서는 이 둘 중 더 많이 사용하는 analytic gradient 계산 방법에 대해 학습하겠습니다.
1.1 Forward propagation
Backpropagation을 알기 전에 알아야하는 것은 Forward propagation입니다.
computational graph를 기준으로 왼쪽부터 오른쪽으로 계산해 나가는 것, 즉 정상적으로 식을 계산하는 것을 Forward propagation(순전파)라고 합니다.
다시말해 입력 데이터를 기반으로 신경망 구조를 따라 입력층(Input Layer)부터 출력층(Output Layer)까지 차례대로 변수들을 계산하고 추론한 결과를 의미합니다.
예를들어 개와 고양이의 사진을 보고 고양이다!라고 사고하는 과정이 순전파이고, 개인지 고양이인지 구별하기까지 학습하는 과정을 역전파라고 합니다.
모델에 입력값을 입력하여 순전파(Forward) 연산을 진행합니다.
이 과정에서 계층(Layer)마다 가중치(Weight)와 편향(Bias)으로 계산된 값이 활성화 함수(Activation Function)에 전달됩니다.
최종 활성화 함수에서 출력값이 계산되고 이 값을 손실 함수(Loss Function)에 실제값과 함께 연산하여 오차(Cost)를 계산합니다.
이러한 Forward pass에서는 각 노드의 계산 결과를 일시적으로 저장합니다.
이는 이후 gradient 계산을 하기위함입니다.
1.2 Backward propagation

인공신경망의 탄생 이후 퍼셉트론을 통해 왼쪽그림과 같이 Linear separable한 문제를 쉽게 해결할 수 있었습니다.
하지만 오른쪽 그림과 같이 XOR 연산자의 Unlinear separable한 문제를 해결할 수 없음이 밝혀졌습니다.
그래서 인경망의 인기가 사그러지다가 1986년 Geoffrey Hinton 연구진이 다층 퍼셉트론을 통해 비선형 분리 XOR 연산 문제를 해결할 수 있게 되었습니다.
하지만 MLP 층의 수가 많아지면서 늘어나는 Weight와 Bias를 수동으로 설정하여 학습시키기에는 한계가 있었습니다.
이를 해결하기 위해 Hinton 교수진이 Back propagtion Algorithm을 제안하면서 MLP를 제대로 학습할 수 있게됩니다.
1.3 computational graph

역전파에 관해 공부하기전 알아야하는 필수개념들을 먼저 설명한 후 진행하겠습니다.
먼저 computational graph라는 프레임워크를 통해 f라는 함수를 표현했습니다.
input값이 x와 w이고, 곱셈노드를 통해 행렬곱셈을 진행하여 score vector를 출력합니다.
그리고 hinge loss node와 regularization항을 계산한 후 최종 L이라는 값을 구하게 됩니다.
이 그래프를 통해 함수를 표현하게됨으로써 backpropagation이라는 기술을 사용할 수 있게 되었습니다.
1.4 chain rule


다음 chain rule, 연쇄법칙입니다. 또 다르게는 합성함수의 미분법이라고도 합니다.
이 체인룰은 변수가 여러 개일 때, 어떤 변수에 대한 다른 변수의 변화율을 알아내기 위해 쓰입니다.
z에 대한 x의 편미분을 구하고 싶은데, 직접적으로 미분이 불가능 할 때 t를 이용하여 구하는것을 보실 수 있습니다.
이러한 연쇄법칙을 사용하면, 편미분을 통해 복잡한 계산을 구할 수 있습니다.
1.5 Partial Derivative


<그림7>의 3차원 그래프는 <그림6> 함수의 그래프인데, y=1로 고정했을 때 절단면이 바로 빨간색 곡선입니다.
저 빨간색 곡선에서 접선의 기울기를 구하는 것이 바로 x에 대한 z의 편미분입니다.
- 편미분과 미분(전미분)의 차이 : 우리가 흔히 알고 있는 미분이란 전미분을 의미하며, 미분이 좀 더 큰 범주이고, 편미분과 여기에 포함된다.
- 예를 들어 설명하면, 집 값(y값)에 영향을 미 치는 변수(variable/x값)가 집의 크기, 집의 위치 등 있을 때,
오직 집의 크기가 집 값에 끼치는 영향을 조사하기 위해선 편미분(Partial Derivative)이 필요하고,
이들의 변수 모두의 변 화가 집 값에 끼치는 영향을 조사하기 위해선 전미분(Full Derivative)이 필요하다.
2. Backpropagation
지금까지 배운 이론을 토대로 역전파(Backpropagation)을 진행해보자.
스칼라 값을 입력으로 받은 간단한 예시를 진행해본 후에, 벡터 값을 입력으로 받았을 때 역전파를 어떻게 수행하는지 자세히 알아보자.
(*예시는 Spring 2017 cs231n 강의 자료에 나와 있는 것을 그대로 가져와 설명만 덧붙였다.)
2.1 Backward propagation

우측 그래프에서 초록 숫자는 local gradient를 의미하며, 빨간 숫자는 global gradient이다. 그래서 우리는 역전파를 통해 빨간 숫자인 global gradient를 찾을 것이다. 역전파를 수행하기 위해 연쇄 법칙(chain rule)을 적용해야 하며, 그러기 위해 편미분 값을 구해야 한다.
우선 좌측 빨간 박스를 보면 식 $q = x + y$이기 때문에 편미분 값은 각각 1을 갖고, 좌측 파란 박스를 보면 $f = qz$이기 때문에 편미분 값은 서로 반대되는 변수 값을 가진다.
편미분도 구했으니 우리는 쉽게 역전파 연산을 수행할 수 있다.

우선 $z$의 global gradient를 구하기 위해서 $f$에 대한 $z$의 변화율을 봐야 하는데 우리는 아까 미리 편미분 값을 구했기 때문에 그 변화율은 $q$다. 따라서 $z$의 global gradient 값은 $q$ 값인 3이 된다.

$q$도 마찬가지로 $f$에 대한 $q$의 변화율은 $z$이기 때문에 $q$의 global gradient는 $z$ 값인 -4가 된다.
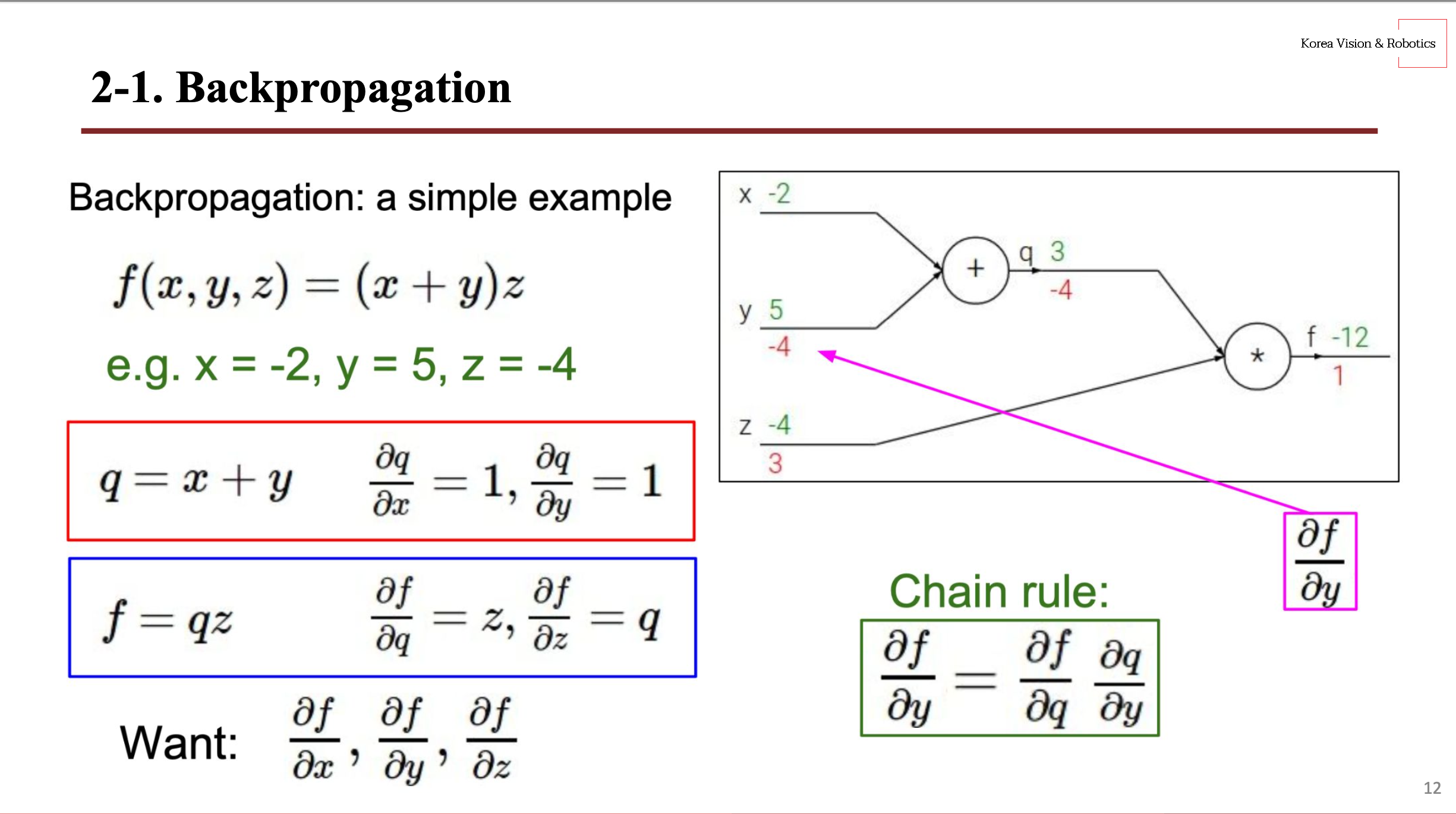
이제 $x$와 $y$를 구하는 것이 관건인데 Chain rule를 사용하면 손쉽게 해결할 수 있다. $f$에 대한 $y$의 변화율을 구하고자 할 때, 한 번에 $y$의 변화율을 알 수 없기 때문에 $f$에서 $q$의 변화율과 $q$에서 $y$의 변화율을 곱하면 $f$에서 $y$의 변화율을 구할 수 있다. 따라서, $z \times 1$을 수행하면 $y$의 global gradient는 -4가 된다.
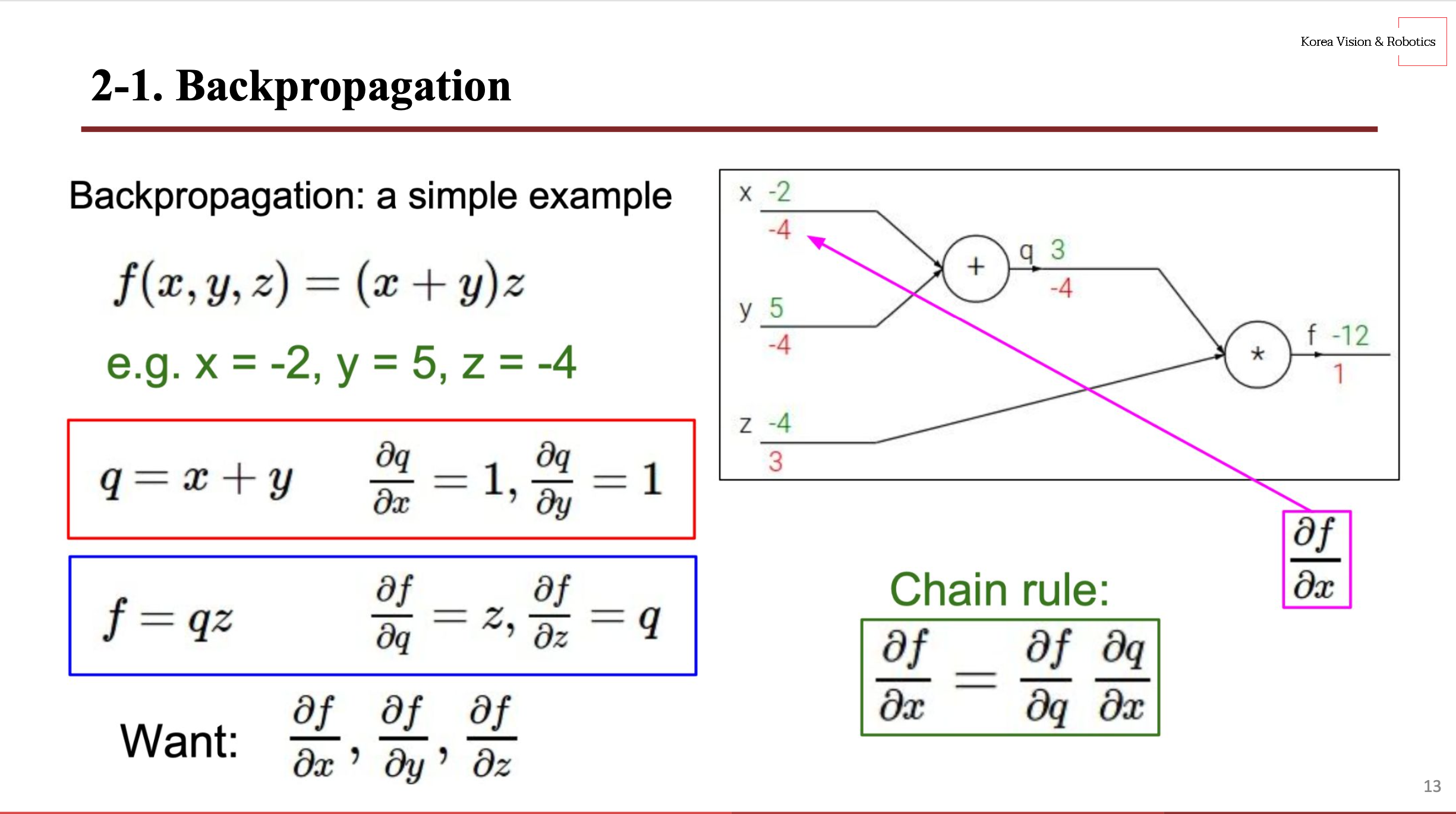
$x$는 $y$의 global gradient 값과 같기 떄문에 -4를 가진다.
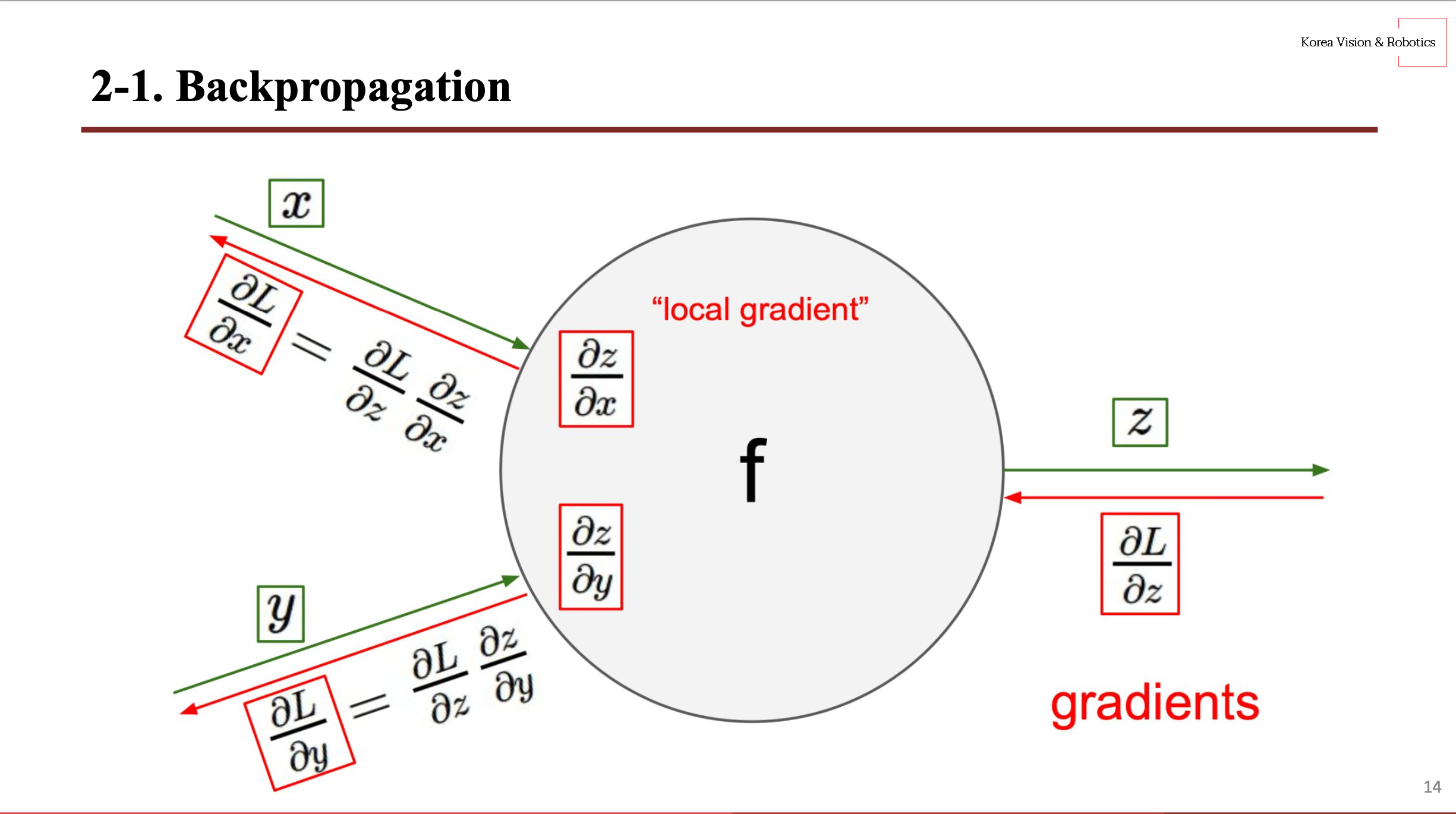
$x$, $y$의 global gradient를 구하기 위해서는 $z$의 global gradient 값과 자기 자신의 local gradient 값을 곱해야 한다. 따라서 자신의 global gradient를 구하기 위해서는 $전단계\;global\;gradient \times 본인\;local\;gradient$라고 할 수 있다.
*번외

추가적으로 gate마다 규칙이 있는데 add gate인 경우 전단계의 global gradient를 그대로 전송하면 되고, max gate 같은 경우에 큰 local gradient 쪽으로 global gradient 값을 넘기고, 반대 쪽에 0을 넘기면 된다. 그리고 mul gate는 global gradient에 local gradient를 반대로 곱해주면 된다.
2.2 Gradients for Vector
이제 간단한 스칼라 예시를 실습해봤으니 벡터일 경우에도 실습을 해보자.

local gradient는 미리 계산해 초록 숫자로 저장되어 있다는 가정 하에 global gradient를 구하자면 초기에는 1.00을 가진다.
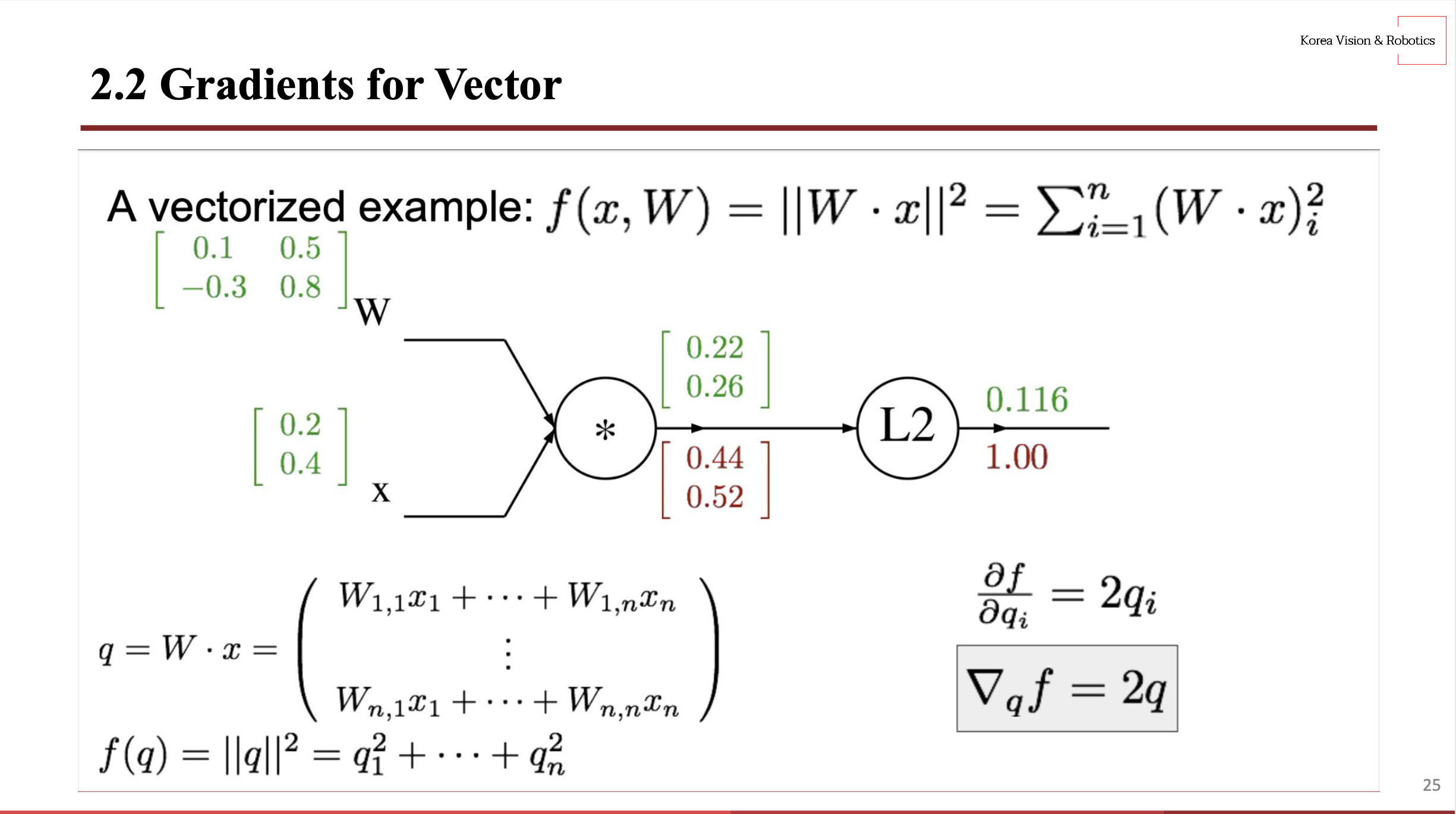
그런 다음 L2에 대한 편미분을 구하자면 $f = q^2$이기 때문에 $2q$이다. 그래서 local gradient에 각각 2를 곱한 값이 global gradient 값이 된다.

$f$에 대한 $W$의 변화율을 알고 싶기 때문에 우리는 $q$의 변화율을 알고 있으니 $q$에서 $W$의 변화율만 구하면 된다.
$q = Wx$이기 때문에 편미분 결과는 $x$이다. 그럼 $W$의 global gradient는 $2qx$인데 (2, 1) * (2, 1)이라 shape이 맞지 않는다. 따라서 $2qx^T$로 바꿔서 계산을 해주면 (2, 2) 크기의 global gradient 값을 얻을 수 있다.

마찬가지로 $q$에 대한 $x$의 변화율은 $W$이며, $x$의 shape와 같은 global gradient를 구하기 위해 $2W^Tq$을 연산하면 된다.
3. Neural Networks
3.1 Neural Networks

우리가 배울 Neural Network는 인간의 Neuron에서 착안해온 모델이다보니 상당부분 Neuron과 닮았습니다.
Neuron은 synapse를 통해 자극이 들어오면 axon을 거친 뒤 그 다음 뉴런으로 신호를 전달합니다.
Neural Network 역시 이와 유사하게 input이 들어오게 되면 가중치를 곱하고 이를 다 더 해준 뒤, 활성함수를 거치게 됩니다. 그리고 그 값을 다음 노드에 전달하는 구조입니다.
그러나 염두해야할 점은 실제 neuron과 neural network가 서로 같다고 이해하면 안된다는 것입니다.
실제로는 neuron의 구조가 더 복잡하므로 개념만 착안해왔다는것을 기억해야합니다.

왼쪽 그림의 경우, 2-layer Neural Net이라고 합니다. 왜 layer가 3개인데 2-layer라고 할까요?
기본적으로 weight를 갖고 있는 것만 layer라고 합니다.
그러면 input layer 같은 경우는 weight를 갖고 있지 않기 때문에 제외가 됩니다.
그래서 2-layer neural network 또는 1-hidden-layer Neural Network라고 부르는 것입니다.
오른쪽 같은 경우도 마찬가지로, 3-layer neural network 또는 2-hidden-layer Neural Network라고 부르게 됩니다.
그리고 위 모델의 마지막 layer와 그 앞의 hidden layer를 보면 모든 노드들이 다 연결되어있는데, 이를 fully connected라고 합니다.
'~2023' 카테고리의 다른 글
| [알고리즘] 그래프 탐색 기법을 코드로 이해하기 (0) | 2023.04.26 |
|---|---|
| [VSCode] ssh 원격 접속하는 방법 (0) | 2023.04.26 |
| [CS231n] Lecture 8. Deep Learning Software (0) | 2023.04.25 |
| [SVM] 서포트 벡터 머신 (Support Vector Machine) (0) | 2023.04.25 |
| [CV] Object Detection 검증 지표 (0) | 2023.04.25 |



